A right-angled triangle has one of its angles set at 90 degrees. A right angle is defined as a 90-degree angle, and a right triangle is defined as a triangle with a right angle. With the Pythagoras rule, the relationship between the various sides of this triangle may be simply understood. The hypotenuse is the longest side of the triangle, and it is opposite the right angle. The right triangles are also classed as isosceles right triangles or scalene right triangles based on the other angle values. Pythagorean triples are also the lengths of the sides of a right angle triangle, such as 3, 4, and 5.
What is the definition of a right triangle?
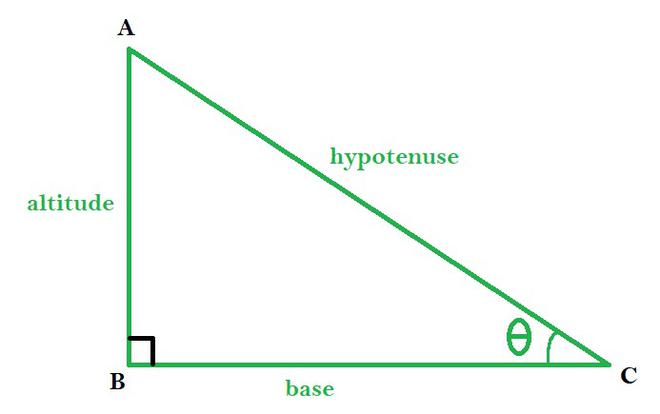
The definition of a right triangle is that it is a right-angled triangle or simply a right triangle if one of the triangle’s angles is a right angle – 90o. Triangle ABC is a right triangle with the base, height, and hypotenuse shown in the illustration. The base is AB, the height is AC, and the hypotenuse is BC. The hypotenuse is the biggest and opposing side of a right triangle, and it is opposite the right angle within the triangle.
We can now recognise the characteristics of a right triangle. Triangle ABC has the following characteristics:
- AC stands for altitude, height, or perpendicularity.
- The basic AC is AB AB A=90o.
- The hypotenuse is the longest side of the right triangle, and it is the side BC opposite the right angle.
The triangular slice of bread, a square piece of paper folded across the diagonal, and the 30-60-90 triangular scale in a geometry box are all instances of right triangles in our daily lives.
Formula for a Right Triangle
Pythagoras, the renowned Greek philosopher, devised a crucial formula for a right triangle. The square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two legs, according to the formula. Pythagoras theorem was named after him. The following is a representation of the right triangle formula: The sum of the squares of the base and height equals the square of the hypotenuse.
We have the following in a right triangle: (Hypotenuse)
2 = (Base)2 + (Base)2 + (Base)2 + (Base (Altitude)
Pythagorean Triplet: The Pythagorean triplets are the three numbers that fulfil the preceding equation.
A Right Triangle’s Perimeter
The circumference of a right triangle is equal to the sum of its three sides. It’s the sum of the right triangle’s base, height, and hypotenuse. The perimeter of the right triangle below equals the sum of the sides BC + AC + AB = (a + b + c) units. The perimeter has a length unit and is a linear value.
Right Triangle Properties
A right triangle’s initial attribute is that one of its angles is 90 degrees. The biggest angle in a right triangle is the 90o angle, which is a right angle. The other two angles are also smaller than 90 degrees or sharp angles. The qualities of the right triangle are mentioned below:
- 90o is always the biggest angle.
- The hypotenuse, which is usually the side opposite the right angle, is the longest side.
- The Pythagoras rule is used to measure the lengths of the sides.
- There can’t be any obtuse angles in it.
Right Triangles Come in a Variety of Shapes
One of the angles of a right triangle is 90o, as we know. As a result, the triangle’s other two angles will be acute angles. Isosceles right triangles and scalene right triangles are two types of special right triangles. An isosceles right triangle is one in which the other two angles are equal, whereas a scalene right triangle is one in which the other two angles have different values. Get in touch with the right experts from Cuemathand learn the concept of obtuse angle triangle.
Also read Struggling With Managing Expenditures? Here’s How What You Can Do to Prevent Loan Build Up
